iact - アイアクト
ネットとリアルを通してECに関わる全ての人をHAPPYに
「ユーザー+クライアント+僕たち」最適な三角形を私たちと構築しませんか?アイアクトは、ECサイト構築におけるあらゆる課題をトータルに解決します。
WORKS 制作実績
-
- 企画
- 制作
- 運営

- ゆず
- http://www.senha-yuzu.jp/
- 公式サイト
-
- 企画
- 制作
- 運営

- ゆず
- http://yuzumoba.jp/
- オフィシャルサイト「ゆずモバ!」
-
- 企画
- 制作
- 運営
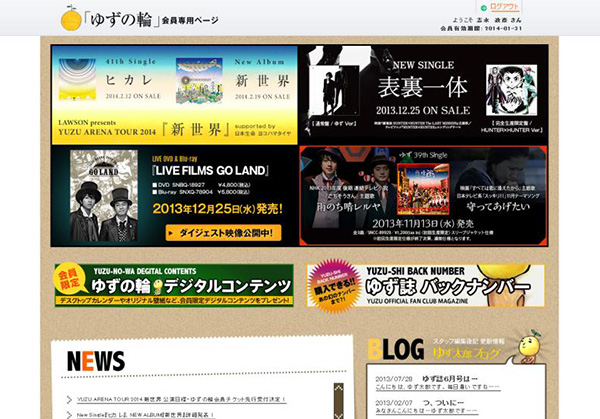
- ゆず
- https://www.senha-yuzu.jp/yuzunowa/public/
- オフィシャルファンクラブ「ゆずの輪」
-
- 企画
- 制作
- 運営

- ゆず
- https://fan-goods.jp/yuzunowa
- オフィシャルグッズストア
-
- 企画
- 制作
- 運営
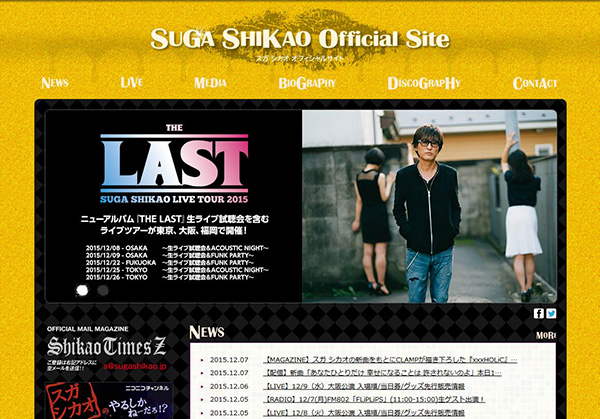
- スガシカオ
- http://www.sugashikao.jp/official.php
- 公式サイト
-
- 企画
- 制作
- 運営

- スガシカオ
- https://fan-goods.jp/sugashikao/
- オフィシャルグッズストア
-
-
- 企画
- 制作
- 運営

- ゆず
- http://www.senha-yuzu.jp/
- 公式サイト
-
-
-
- 企画
- 制作
- 運営

- ゆず
- http://yuzumoba.jp/
- オフィシャルサイト「ゆずモバ!」
-
-
-
- 企画
- 制作
- 運営

- ゆず
- https://www.senha-yuzu.jp/yuzunowa/public/
- オフィシャルファンクラブ「ゆずの輪」
-
-
-
- 企画
- 制作
- 運営

- ゆず
- https://fan-goods.jp/yuzunowa
- オフィシャルグッズストア
-
-
-
- 企画
- 制作
- 運営

- スガシカオ
- http://www.sugashikao.jp/official.php
- 公式サイト
-
-
-
- 企画
- 制作
- 運営

- スガシカオ
- https://fan-goods.jp/sugashikao/
- オフィシャルグッズストア
-
-
-
- 企画
- 制作
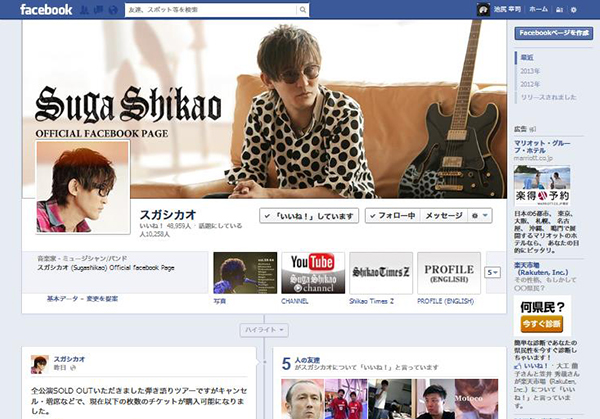
- スガシカオ
- https://www.facebook.com/Shikaosuga
- オフィシャルFacebookファンページ
-
-
-
- 運営

- スガシカオ
- オフィシャルメールマガジン
-
-
-
- 企画
- 制作
- 運営
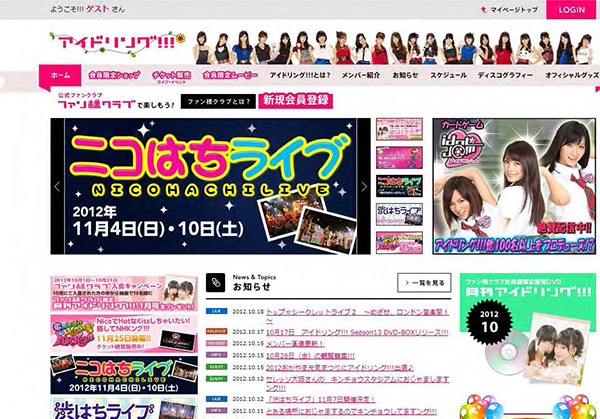
- アイドリング!!!
- 公式サイト
-
-
-
- 企画
- 制作
- 運営
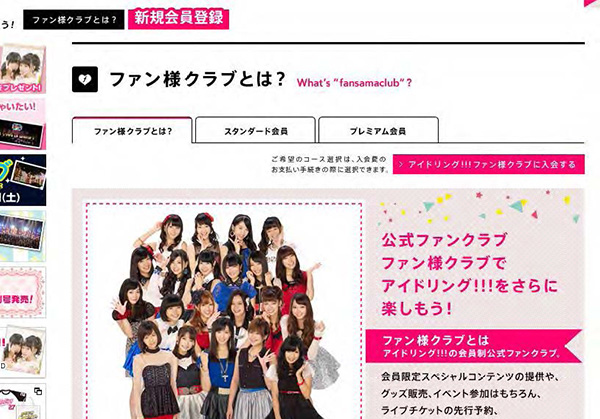
- アイドリング!!!
- オフィシャルファンクラブ「ファン様クラブ」
-
-
-
- 企画
- 制作
- 運営
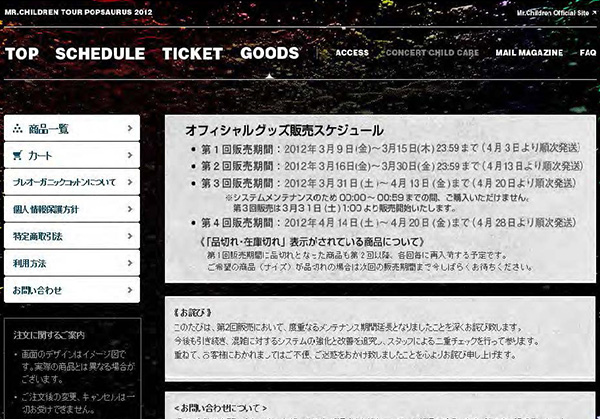
- Mr.children
- オフィシャルグッズストア
-
-
-
- 企画
- 制作
- 運営

- レミオロメン
- ツアー限定公式グッズサイト
-
-
-
- 企画
- 制作
- 運営

- 大阪王将
- 通販サイト
-
-
-
- 企画
- 制作
- 運営

- 東京スカパラダイスオーケストラ
- ツアー限定公式グッズサイト
-
-
-
- 企画
- 制作
- 運営

- 熊田曜子バスエッセンス
- 通販サイト
-
-
-
- 企画
- 制作
- 運営

- 一青窈
- https://fan-goods.jp/hitotoyo/
- ツアー限定公式グッズサイト
-
-
-
- 企画
- 制作
- 運営

- 2PM
- オフィシャルグッズストア
-
-
-
- 企画
- 制作
- 運営

- 氣志團
- https://fan-goods.jp/kishidan/
- オフィシャルグッズストア
-
-
-
- 企画
- 制作
- 運営

- Nico touches the walls
- 公式サイト
-
-
-
- 企画
- 制作
- 運営

- ORANGERANGE
- http://orangerange.com/
- 公式サイト
-
-
-
- 企画
- 制作
- 運営
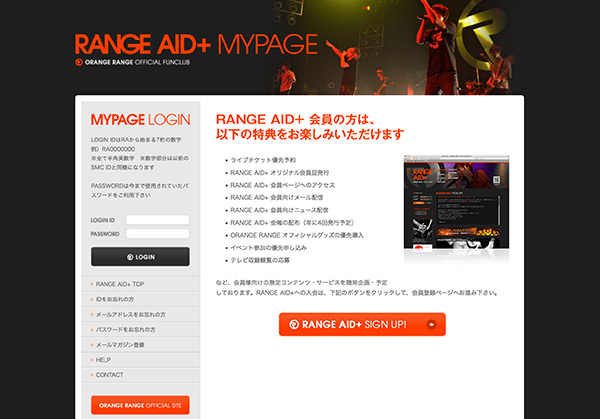
- ORANGERANGE
- https://orangerange.com/mypage/member/
- オフィシャルファンクラブ「RANGE AID+」
-
-
-
- 企画
- 制作
- 運営

- ORANGERANGE
- https://orangerange.com/goods/
- オフィシャルグッズストア
-
-
-
- 企画
- 制作
- 運営
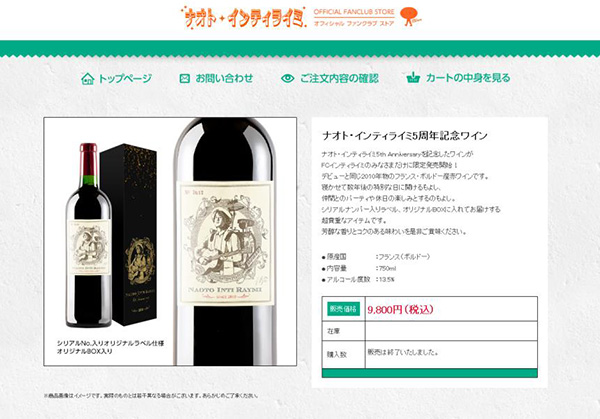
- ナオト・インティライミ
- オフィシャルグッズストア
-
-
-
- 企画
- 制作
- 運営

- シクラメン
- https://fan-goods.jp/shikura/
- オフィシャルグッズストア
-
-
-
- 企画
- 制作
- 運営
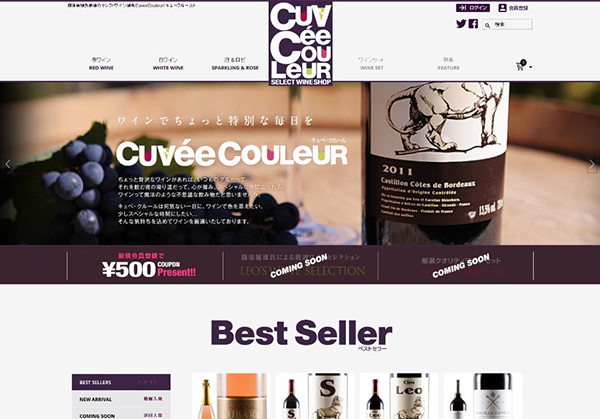
- CuveeCouleur
- https://www.c-couleur.com/
- 公式通販サイト
-
-
-
- 企画
- 制作
- 運営

- ラブライブ!
- https://fan-goods.jp/lovelive_6th/
- 公式通販サイト
-
-
-
- 企画
- 制作
- 運営

- 長淵剛
- 公式通販サイト
-
-
-
- 企画
- 制作
- 運営
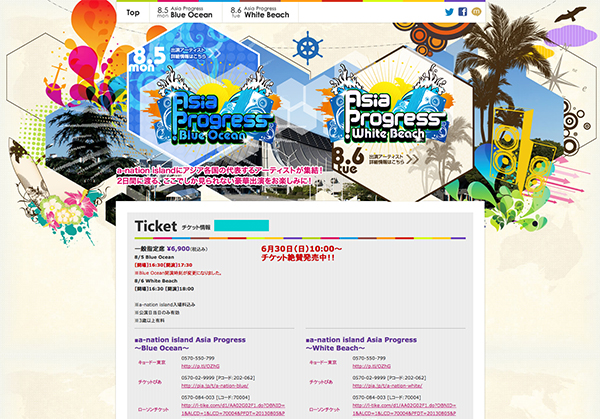
- a-nation
- http://www.asia-progress2013.com/
- オフィシャルサイト
-
SERVICE サービス
商品企画からシステム、サーバー、サイト構築、販売管理、物流管理、商品発送までECに関わるサービス全てをご提供致します。
-
- ECサイト運営代行
- 物流代行、サーバ管理など、ECサイト運営にともなう全プロセスをワンストップでご提供いたします。
-
- ECコンサルティング
- これまでのECサイト運営・構築でつちかった、売れるECサイトのノウハウをご提供いたします。
-
- マーケティング(調査・分析)
- 各種データの集計はもちろん、RFM分析やコンバージョン分析などのマーケティングデータを提供いたします。
-
- 広告プロモーション
- 毎月の成果をレポートと併せてご報告し、PDCAサイクルを回しながら最適化を進めていきます。
-
- 販売戦略立案
- 各種調査から改善提案、コンテンツ制作、システム開発、運用までのプロジェクト全体を見据えた販売戦略を立案いたします。
-
- 物流サービス代行
- 配送料・人件費・場所代・在庫管理など物流サービス代行を利用することでコストの削減が可能です。
-
- EC人材派遣
- ネットショップを運営するには規模にもよりますが様々な人材が必要です。EC運営に特化した人材を派遣いたします。
-
- ファンクラブサイト運営・構築
- エンターテイメント系ファンクラブの効率的で安定したFCサイト運用をサポートいたします。
-
- 各種サイト制作
- 様々な分野のウェブサイト(スマートフォン・携帯・PC)の制作を行っています。
CONTACT お問い合わせ
サイト制作や運用線略立案、その他様々なご相談でもお気軽にご連絡ください。
COMPANY 会社概要
〒106-0031 東京都渋谷区恵比寿西 1-29-5 代官山TYK302
TEL:03-6427-8042 FAX:03-6427-8043
- インターネットアプリケーション開発
- データベースシステム構築
- WEBコンテンツ企画・運営
- ECサイト企画・開発・制作・運用
- システムコンサルティング業務
- システム保守サポート
- ネットワークシステム構築業務
- Web広告・プロモーション業務
- モバイルコンテンツ企画・開発
- 株式会社サイバード
- 讀賣テレビ放送株式会社
- 関西テレビ放送株式会社
- エイベックス・グループ・ホールディングス株式会社
- 株式会社サイバーエージェント
- 株式会社カラーズ
- ソフトバンクモバイル株式会社
- KDDI株式会社
- 株式会社NTTドコモ
- 株式会社イートアンド(旧大阪王将)
- 株式会社スパイスレコーズ
- 株式会社 アーティマージュ
敬称略・順不同